Master the Rules for Solving Mathematical Expressions
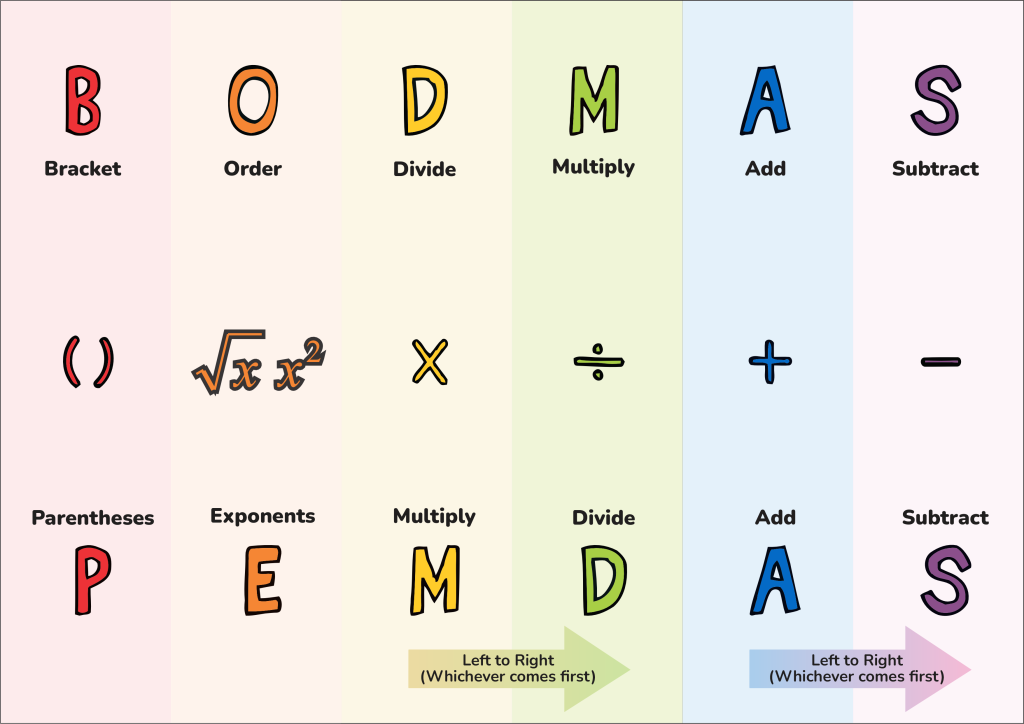
The Order of Operations is a set of rules that tells us which calculations to perform first when solving mathematical expressions with multiple operations. Without these rules, different people would get different answers to the same problem!
(Used in USA)
"Please Excuse My Dear Aunt Sally"
(Used in UK, India, Australia)
Both methods give the same result!
Multiplication and Division have the same priority — work from LEFT to RIGHT.
Addition and Subtraction have the same priority — work from LEFT to RIGHT.
❌ Common Mistake: Don't always do multiplication before division!
❌ Common Mistake: Don't always do addition before subtraction!
Solve everything inside ( ), [ ], and { } from innermost to outermost.
Example: \( (3 + 5) \times 2 = 8 \times 2 = 16 \)
Calculate powers, square roots, and other exponents.
Example: \( 3^2 + 4 = 9 + 4 = 13 \)
Perform whichever comes first as you read from left to right.
Example: \( 12 \div 4 \times 3 = 3 \times 3 = 9 \)
Perform whichever comes first as you read from left to right.
Example: \( 10 - 3 + 5 = 7 + 5 = 12 \)
Solve: \( 6 \times 4 + 8 \div 2 \)
Step 1: Multiply and divide first (left to right)
\( 6 \times 4 = 24 \)
Now we have: \( 24 + 8 \div 2 \)
\( 8 \div 2 = 4 \)
Now we have: \( 24 + 4 \)
Step 2: Add
\( 24 + 4 = 28 \)
✓ Answer: 28
Solve: \( (8 + 5) - 3 \times 2^2 \)
Step 1: Parentheses first
\( (8 + 5) = 13 \)
Now we have: \( 13 - 3 \times 2^2 \)
Step 2: Exponents
\( 2^2 = 4 \)
Now we have: \( 13 - 3 \times 4 \)
Step 3: Multiplication
\( 3 \times 4 = 12 \)
Now we have: \( 13 - 12 \)
Step 4: Subtraction
\( 13 - 12 = 1 \)
✓ Answer: 1
Solve: \( 18 \div 9 \times 2 \)
⚠️ Many students get this wrong!
Step 1: Work left to right (division comes first)
\( 18 \div 9 = 2 \)
Now we have: \( 2 \times 2 \)
Step 2: Multiply
\( 2 \times 2 = 4 \)
✓ Answer: 4 (NOT 1!)
❌ If you did multiplication first: \( 18 \div (9 \times 2) = 18 \div 18 = 1 \) — This is WRONG!
Solve: \( 3 + 6 \times (5 + 4) \div 3 - 7 \)
Step 1: Parentheses
\( (5 + 4) = 9 \)
Now: \( 3 + 6 \times 9 \div 3 - 7 \)
Step 2: Multiplication and Division (left to right)
\( 6 \times 9 = 54 \)
Now: \( 3 + 54 \div 3 - 7 \)
\( 54 \div 3 = 18 \)
Now: \( 3 + 18 - 7 \)
Step 3: Addition and Subtraction (left to right)
\( 3 + 18 = 21 \)
\( 21 - 7 = 14 \)
✓ Answer: 14
Wrong Thinking: "PEMDAS says M comes before D, so multiply first."
Correct Rule: Multiplication and Division have equal priority. Work left to right!
Example: \( 8 \div 2 \times 4 \)
❌ Wrong: \( 8 \div (2 \times 4) = 8 \div 8 = 1 \)
✓ Correct: \( (8 \div 2) \times 4 = 4 \times 4 = 16 \)
Wrong Thinking: "A comes before S in PEMDAS."
Correct Rule: Addition and Subtraction have equal priority. Work left to right!
Example: \( 10 - 3 + 5 \)
❌ Wrong: \( 10 - (3 + 5) = 10 - 8 = 2 \)
✓ Correct: \( (10 - 3) + 5 = 7 + 5 = 12 \)
Correct Rule: Always work from the innermost parentheses outward.
Example: \( 5 + [3 \times (2 + 4)] \)
✓ Step 1: \( (2 + 4) = 6 \) → \( 5 + [3 \times 6] \)
✓ Step 2: \( [3 \times 6] = 18 \) → \( 5 + 18 \)
✓ Step 3: \( 5 + 18 = 23 \)
Correct Rule: PEMDAS/BODMAS applies inside parentheses too!
Example: \( (3 + 2 \times 4) \)
❌ Wrong: \( (5 \times 4) = 20 \)
✓ Correct: \( (3 + 8) = 11 \) (multiply before adding, even inside parentheses!)
PEMDAS: "Please Excuse My Dear Aunt Sally"
BODMAS: "Big Oranges Don't Make Any Sense"
GEMS: "Grouping, Exponents, Multiply/Divide, Add/Subtract"
If you're unsure about the order, use parentheses to show what should be calculated first. This makes your work clearer and helps avoid mistakes.
Example: \( 2 + 3 \times 4 \) can be written as \( 2 + (3 \times 4) \) to clarify.
As you work through a problem, underline or highlight the operation you're about to perform. This helps you track your progress and catch errors.
Remember that MD and AS are pairs that work together left to right:
Parentheses → Exponents → (MD) Left to Right → (AS) Left to Right
Most scientific calculators follow PEMDAS/BODMAS. Use them to verify your answer, but always work through the problem by hand first to understand the process.
Sometimes it helps to rewrite \( a \div b \) as \( a \times \frac{1}{b} \). This can make complex expressions easier to understand.
Example: \( 8 \div 2 \times 4 = 8 \times \frac{1}{2} \times 4 = 16 \)
Try these problems on your own, then click to reveal the solutions!
Click to reveal solution ▼
Click to reveal solution ▼
Click to reveal solution ▼
Click to reveal solution ▼
Click to reveal solution ▼
| Order | Operation | Symbol/Example | Direction |
|---|---|---|---|
| 1st | Parentheses/Brackets | \( ( ) [ ] \{ \} \) | Innermost first |
| 2nd | Exponents/Orders | \( x^2, \sqrt{x}, x^n \) | Top to bottom |
| 3rd | Multiplication & Division | \( \times \div \) | Left to Right |
| 4th | Addition & Subtraction | \( + - \) | Left to Right |
Parentheses → Exponents → Multiply/Divide (Left to Right) → Add/Subtract (Left to Right)
The order of operations ensures everyone solves math problems the same way and gets the same answer. Master this, and you'll avoid 90% of common calculation errors!
