Mathematics is all around us, and understanding the right mathematical rules can greatly enhance our ability to solve problems efficiently. One pivotal rule in the realm of mathematics, especially when multiple operations are involved in an equation, is the PEMDAS rule.
You might be well-acquainted with basic operations like addition, division, subtraction, and multiplication, but how do you prioritize these when they appear together? PEMDAS is a fundamental rule used not only in solving complex mathematical problems but also extensively in computer programming.
What is PEMDAS?
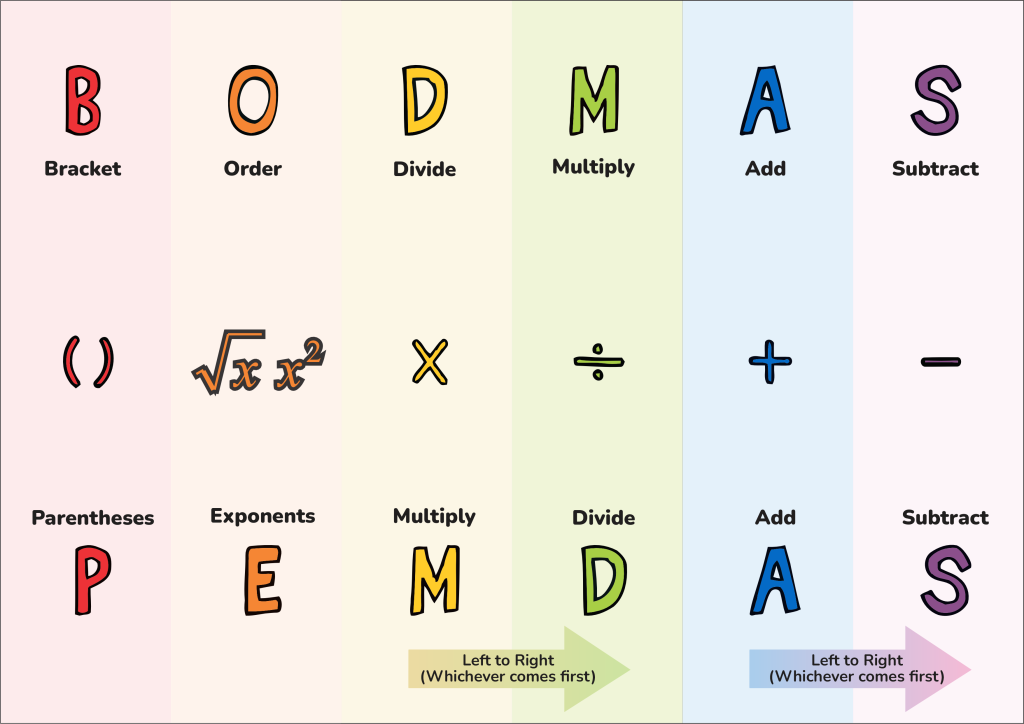
PEMDAS is an acronym that helps us remember the order of operations to be followed while solving expressions with multiple operations. It stands for
P – Parentheses
E – Exponents
M – Multiplication
D – Division
A – Addition, and
S – Subtraction.
Different countries might use various acronyms to describe the order of operations. In Canada, for instance, it’s referred to as
BEDMAS (Brackets, Exponents, Division, Multiplication, Addition, and Subtraction)
Others may know it as
BODMAS (B – Brackets, O – Order (exponent or power) or Division, Multiplication, Addition, and Subtraction)
GEMDAS (G – Grouping) and the rest of the letters representing each operation as above.
Illustrating PEMDAS Through Examples
Consider the following situation where two individuals, Tom and Jerry, solve the same mathematical expression, but each uses a different method:
Tom’s Method:
5 + 2 × 3
Tom adds the 5 and 2 together first, to obtain 7.
= 7 × 3
He then proceeds to multiply the 7 by 3.
= 21
Jerry’s Method:
5 + 2 × 3
Tom multiplies 2 by 3 first, to obtain 6.
= 5 + 6
He then adds 5 and 6, and gets 11
= 11
As you can see, Tom and Jerry arrived at different answers. In mathematics, there is only one correct answer for any given expression (unless you’re solving trigonometric functions). Using PEMDAS, we can determine the right solution.
PEMDAS Rules in Action
Let’s follow the PEMDAS rules: We start with Parentheses, then Exponents. Following that, we perform Multiplication and Division from left to right, and finally, Addition and Subtraction from left to right. Following this order ensures the correct answer.
Here’s another example to deepen your understanding:
Expression:
4 + 3[8 – 2(6 – 3)] ÷ 2
Steps:
By following PEMDAS strictly, you ensure that all calculations are performed in the correct order, leading to accurate results.
Using PEMDAS to Excel in Math
PEMDAS isn’t just a rule but a crucial strategy that, when applied correctly, can help you excel in your mathematics classes and beyond. Understanding and practicing this rule can simplify complex problems and increase your efficiency in solving them.
Explaining the BODMAS rule, which is a mnemonic similar to PEMDAS for remembering the order of operations in mathematics. BODMAS stands for Brackets, Order, Divide, Multiply, Add, and Subtract.
BODMAS Explained:
P – Parentheses
The order is crucial because performing these operations out of sequence can lead to incorrect results. The left-to-right rule for operations at the same level (like Divide and Multiply, Add and Subtract) is important and is a common feature shared with PEMDAS.
PEMDAS, on the other hand, stands for Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. While it may seem that Multiplication comes before Division and Addition before Subtraction in PEMDAS, the operations at each level (Multiplication and Division, Addition and Subtraction) are actually carried out from left to right, similar to BODMAS.
Example Using BODMAS:
Let’s apply BODMAS to the same example used previously for PEMDAS to show they are equivalent:
Expression:
4+3[8−2(6−3)]÷2
Steps:
So, whether you use BODMAS or PEMDAS, the correct order of operations will guide you to the right answer. In this case, the final result is 7.
Keep practicing and applying the BODMAS or PEMDAS rule to different problems you encounter in your studies or in everyday life, and watch your proficiency in mathematics grow!
Until next time, happy calculating!
NUM8ERS is one of finest tutoring institutes in UAE, Located in Al Barsha 1, Dubai. Close to DUBAI AMERICAN ACADEMY.